Introduction � la cryptographie
ArticleCategory:
System Administration
AuthorImage:

TranslationInfo:[Author and translation history]
original in fr Pierre Loidreau
AboutTheAuthor
Pierre est Enseignant-Chercheur � l'ENSTA (Ecole Nationale
Sup�rieure de Techniques Avanc�es). Son domaine de recherche concerne
les "cryptosyst�mes" fond�s sur la th�orie des codes correcteurs d'erreurs. Il
pratique Linux tous les jours... et le tennis fr�quemment.
Abstract:
Cet article a �t� publi� dans un num�ro sp�cial sur la s�curit� de Linux
Magazine France. L'�diteur, les auteurs, les traducteurs ont aimablement
accept� que tous les articles de ce num�ro hors-s�rie soient publi�s dans
LinuxFocus. En cons�quence, LinuxFocus vous "offrira" ces articles au fur et
� mesure de leur traduction en Anglais. Merci � toutes les personnes qui se
sont investies dans ce travail. Ce r�sum� sera reproduit pour chaque article
ayant la m�me origine.
ArticleIllustration:

ArticleBody:[The article body]
Pourquoi la cryptographie - 2500 ans d'histoire av�r�e.
L'origine de la cryptographie remonte sans doute aux origines de
l'homme, d�s que ceux-ci apprirent � communiquer. Alors, ils durent
trouver des moyens d'assurer la confidentialit� d'une partie de leurs
communications. Dans l'�gypte ancienne, l'�criture joua parfois ce
r�le. Cependant la premi�re attestation de l'utilisation d�lib�r�e de
moyens techniques permettant de chiffrer les messages vint de la
Gr�ce, vers le VI�me si�cle avant J.C, et se nomme ``scytale''. Le
scytale �tait un b�ton. L'exp�diteur enroulait une bandelette autour
et �crivait longitudinalement sur le b�ton. Puis il d�roulait la
bandelette et l'exp�diait au destinataire. Sans la connaissance du
diam�tre du b�ton qui jouait le r�le de cl�, il �tait impossible de
d�chiffrer le message.
Plus tard, les arm�es romaines utilis�rent pour communiquer le
chiffrement de C�sar consistant en un d�calage de l'alphabet de trois
lettres.
Puis, pendant pr�s de 19 si�cles, on assista au d�veloppement plus ou
moins ing�nieux de techniques de chiffrement exp�rimentales dont la
s�curit� reposait essentiellement dans la confiance que leur
accordaient les utilisateurs. Au 19�me si�cle, Kerchoffs posa les
principes de la cryptographie moderne. L'un des principaux pose que
la s�curit� d'un syst�me de chiffrement ne r�sidait que dans la cl� et
non dans le proc�d� de chiffrement.
D�sormais, concevoir des syst�mes cryptographiques devait
r�pondre � ces crit�res. Cependant,
il manquait encore � ces syst�mes une assise math�matique donnant des
outils qui permette de mesurer,
de quantifier leur r�sistance � d'�ventuelles attaques, et pourquoi pas de trouver le ``saint Graal'' de la cryptographie : le syst�me inconditionnellement s�r. En 1948 et 1949, deux articles de Claude Shannon,
``A mathematical theory of communication'' et surtout
``The communication theory of secrecy systems'' donn�rent des assises scientifiques � la cryptographie en balayant espoirs et pr�jug�s. Shannon prouva que le chiffrement de Vernam introduit quelques dizaines d'ann�es plus t�t -- encore appel� one-time pad -- �tait le seul syst�me inconditionnellement s�r. Cependant ce syst�me est impraticable. C'est pourquoi, de nos jours pour �valuer la s�curit� d'un syst�me on s'int�resse plut�t � la s�curit� calculatoire. On dit qu'un syst�me de chiffrement � cl� secr�te est s�r si aucune attaque connue ne fait beaucoup mieux en complexit� que la recherche exhaustive sur l'espace des cl�s.
L'AES (Advanced Encryption Standard)
Tr�s r�cemment, en octobre 2000, un nouveau standard de chiffrement � cl� secr�te fut �lu parmi
15 candidats par la NIST (National Institute of Standards and Technology) afin de remplacer le viellissant DES dont la taille des cl�s devenait trop petite. L'algorithme choisit pour devenir l'AES est le Rijndael, du nom
condens� de ses concepteurs, Rijmen et Daemen.
Celui-ci est un syst�me de chiffrement dit ``par blocs'' car les
messages sont chiffr�s par blocs entiers, qui ici sont de 128 bits.
Il existe plusieurs versions du syst�me utilisant des cl�s de 128, 192
ou 256 bits.
Pour information, le DES chiffre des blocs de 64 bits avec une cl� de
56 bits seulement. Le triple DES utilis� commun�ment jusqu'alors chiffre des blocs de
64 bits avec une cl� de 112 bits.
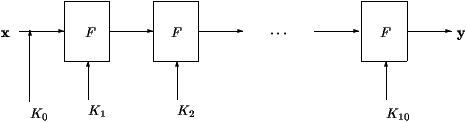
Table 1: It�rations de l'AES
Le principe de fonctionnement de l'AES est d�crit dans la figure 1.
En premier lieu, on ajoute bit � bit le message avec la cl� secr�te K0.
Puis, comme pour tous les algorithmes de chiffrement
par blocs, on it�re une fonction F, param�tr�e par des sous-cl�s qui sont obtenues de la cl�
ma�tre par un algorithme de cadencement de cl�s.
Dans le cas d'AES, on it�re 10 fois la fonction F.
- La fonction F it�r�e lors du chiffrement est d�crite figure 2. Celle-ci
prend en entr�e des blocs de 128 bits r�partis sur 16 octets. Tout d'abord, on applique �
chaque octet la m�me permutation S. Ensuite on applique aux 16 octets
une seconde permutation P. Au r�sultat obtenu, on ajoute alors bit
� bit la sous-cl� de 128 bits obtenue par l'algorithme de cadencement de cl�.
- L'algorithme de cadencement de cl� permet de calculer la cl� Ki du i�me tour en fonction
de la sous-cl� Ki-1 du (i-1)�me tour, K0 �tant la
cl� secr�te. Celui-ci est d�crit dans la figure 3.
Les 16 octets de la cl� Ki-1 sont pris 4 � 4. Aux 4 derniers octets, on commence par
faire subir une permutation, puis on r�utilise la m�me permutation S que celle de la
fonction F afin de permuter les bits de chaque octet. Ensuite, on additionne au premier octet du
nouvel ensemble l'�l�ment ai. Cet �l�ment
est un octet qui d�pend du num�ro i du tour consid�r�.
Enfin pour obtenir Ki, on ajoute bit � bit les 4 octets
obtenus aux 4 premiers octets de Ki-1, puis le r�sultat obtenu est additionn� aux 4 octets suivants et ainsi de suite.
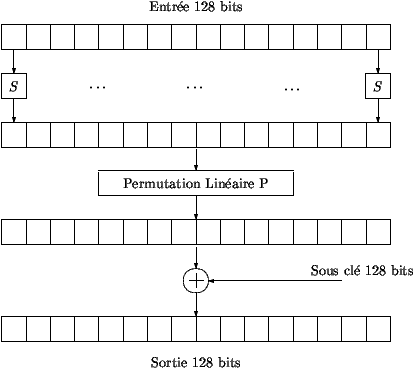
Table 2: Fonction F
Voici bri�vement comment sont construites les permutations et � quoi correspond
la constante ai. Techniquement et
pour des soucis de facilit�s, un octet peut �tre consid�r� comme un �l�ment d'un
ensemble � 256 �l�ments appel� corps fini,
sur lequel existent toutes sortes d'op�rations simples, notamment des op�rations d'additions, de multiplication et d'inversion. La permutation S sus-mentionn�e correspond � l'inversion sur cet ensemble.
La permutation P est sp�cifi�e comme �tant une op�ration tr�s simple, s'implantant
facilement. L'�l�ment ai correspond � l'�l�vation � la puissance i d'un �l�ment du corps. De telles consid�rations permettent d'impl�menter tr�s efficacement l'AES.
Comme l'AES ne comporte que des op�rations tr�s simples sur les
octets, cette propri�t� lui procure deux �normes avantages :
- l'implantation, m�me software d'un AES est extr�mement rapide. Par exemple, une implantation en C++ sur un pentium � 200Mhz permet de chiffrer 70Mbits/s ;
- la r�sistance d'AES � la cryptanalyse diff�rentielle et
lin�aire ne d�pend pas du choix de S-box comme dans le
DES, qui avaient �t� suspect�es d'avoir �t� pi�g�es par la
NSA. En effet, toutes les op�rations effectu�es sont des
op�rations simples.
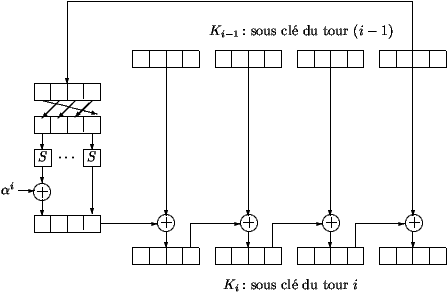
Table 3: algorithme de cadencement de cl�s
Cryptographie � cl� publique
En 1976, Diffie et Hellman publi�rent un article ``New Directions in
Cryptography'' qui fit l'effet d'une
bombe dans la communaut� des cryptographes, en introduisant le concept de cryptographie � cl� publique.
Les algorithmes de chiffrement � cl� secr�te, les seuls connus
jusqu'alors ne satisfaisaient plus les les besoins nouveaux qui
apparurent parall�lement � l'explosion des moyens de communication
tr�s impersonnels -- le d�veloppement des r�seaux par exemple.
La solution tout � fait novatrice qu'ils propos�rent fut d'introduire la notion de fonction � sens unique avec trappe ou trapdoor one-way function. C'est une fonction qui se calcule facilement dans un sens, mais qui est calculatoirement impossible � inverser si l'on ne conna�t pas un secret appel� trappe,
bien que cette fonction soit connue de tous.
La cl� publique est alors la fonction, tandis que la trappe, connue d'un nombre restreint d'utilisateurs
s'appelle cl� priv�e. Ainsi naquit le monde d'Alice, Bob et compagnie. Alice et Bob sont deux personnes
qui cherchent � communiquer de maniere int�gre tandis que des personnes peuvent s'interposer, �couter ou
m�me brouille le canal de communication.
Pour d�chiffrer le message le destinataire inverse la fonction en utilisant la trappe.
Le plus bel exemple de cryptosyst�me � cl� publique et sans conteste le plus simple apparut juste deux ans plus tard en 1978. Il est d� � Rivest, Shamir et Adleman d'o� le nom RSA. Il s'appuie sur la difficult� de factoriser deux entiers. La cl� priv�e est constitu� du triplet (p,q,d) o� p et q sont deux nombres premiers de m�me taille, et ou d est un nombre entier premier avec p-1 et avec q-1. La cl� publique se compose de la paire (n, e ).
o� n=pq et o� e est l'inverse de d modulo (p-1)(q-1), i.e.
ed = 1 mod(p-1)(q-1).
Supposons qu'Alice souhaite envoyer un message chiffr� avec la cl� publique de Bob (n,e). D'abord, elle
transforme le message en un nombre m inf�rieur au modulo n. Ensuite elle calcule
c = me modn,
et envoie c � Bob. Celui-ci dont la cl� publique est (p,q,d) calcule
cd modn = med modn = m.
Dans le cas de RSA, la fonction � sens unique avec trappe que l'on
consid�re est la fonction qui affecte � un nombre x <n
la valeur xe modn.
Depuis le syst�me de chiffrement RSA, bien d'autres syst�mes de
chiffrement � cl�
publique furent d�velopp�s. Un des plus en vogue
actuellement, et un concurrent s�rieux de RSA est un syst�me de chiffrement
fond� sur des probl�mes de calcul de logarithmes discrets.
De l'utilisation moderne de la cryptographie
En r�alite, l'int�r�t de la cryptographie � cl� publique est de pourvoir � tout un nombre de probl�mes
de s�curit�, et d'offrir une tr�s grande souplesse. Celle-ci permis
notamment de trouver des solutions
aux probl�mes d'authentification :
- L'identification de personnes :
avec l'apparition des moyens de communication impersonnels,
Alice veut �tre s�re que la personne avec laquelle elle
communique ne triche pas sur son identit�, c'est-�-dire que quelqu'un
pr�tendant �tre �Bob� est bien Bob en r�alit�. Pour ce faire, elle
utilise ce qu'on appelle un protocole d'identification. Il en existe une
multitude reposant sur les m�mes principes qui r�gissent RSA ou les syst�mes utilisant des
propri�t�s de logarithme discret.
- L'authentification de documents : une autorit� peut
authentifier des documents par l'interm�diaire d'une signature
num�rique. La signature consiste �
adjoindre au document un certain nombre de bits qui sont calcul�s en
fonction du document et de l'autorit�, et en g�n�ral sont hach�s par une fonction de hachage de type
MD5 ou SHA. De plus, toute personne ayant
acc�s au document, doit pouvoir v�rifier que la signature est bien
celle de l'autorit�. Pour ce faire on utilise ce que l'on appelle des sch�mas de signature.
Un des plus c�l�bre, le sch�ma de signature ElGamal repose encore sur des probl�mes de recherche de
logarithme discret.
En outre, comme la cryptographie � cl� secr�te, la cryptographie � cl� publique permet d'�laborer des
syst�mes de chiffrement, d'assurer la confidentialit� des
communications.
Supposons qu'Alice souhaite communiquer avec Bob de mani�re
priv�e. Alice trouve dans l'annuaire la cl� publique de
Bob, puis chiffre le message avec cette cl�. Quand Bob re�oit le
message chiffr�, il utilise sa cl� priv�e afin de
d�chiffrer le message et de retrouver le texte
clair. Les deux cl�s ont des r�les fondamentalement
diff�rents, et c'est la raison pour laquelle on parle encore pour
de tels syst�mes de cryptosyst�mes asym�triques, par
opposition aux cryptosyst�mes � cl� secr�te utilisant la m�me cl�
en chiffrement et en d�chiffrement et qui sont �galement appel�s
cryptosyst�mes sym�triques.
La cryptographie � cl� publique poss�de ici aussi un avantage
majeur sur la cryptographie � cl� secr�te.
En effet, si n utilisateurs souhaitent
communiquer par le biais d'un cryptosyst�me � cl� secr�te, chacun
d'eux doit disposer d'une cl� diff�rente par personne du
groupe. Il faut donc pouvoir g�rer en tout n(n-1) cl�s.
Sachant que n peut �tre de l'ordre de plusieurs milliers, il
faut g�rer des fichiers de plusieurs millions de cl�s. De plus, ajouter un utilisateur au
groupe n'est pas une mince affaire, puisqu'il faut alors engendrer
n cl�s pour que le nouvel utilisateur puisse communiquer avec
les autres membres du groupe, puis distribuer les nouvelles cl�s �
tout le groupe. En revanche, dans le cas d'un
cryptosyst�me asym�trique, on stocke
les n cl�s publiques des utilisateurs dans un annuaire. Pour rajouter un
utilisateur, il suffit qu'il mette sa cl� publique dans l'annuaire.
Cl� publique ou cl� secr�te, un compromis
Dans le paragraphe pr�c�dent, on a vu que la cryptographie � cl�
publique apportait une solution � bien plus de probl�mes que la
cryptographie � cl� secr�te. Alors on peut se demander quelle est
l'utilit� de l'AES dans ce cas. Il existe deux raisons fondamentales �
ce choix.
- D'une part une raison pratique. En effet, la plupart des
syst�mes de chiffrement � cl� publique sont tr�s lents. Le RSA est
par exemple plusieurs centaines de fois plus lent que l'AES en
programmation logicielle et est compl�tement hors du coup en
implantation mat�rielle. A notre �poque o� la vitesse de
transmission de l'information constitue un enjeu crucial,
l'algorithme de chiffrement ne doit pas �tre le facteur limitant.
- D'autre part du point de vue de la s�curit� se posent des
probl�mes relatifs � la structure m�me des syst�mes de chiffrement
� cl� publique.
Il est frappant de constater que la taille des cl�s n�cessaire en
cryptographie � cl� publique pour assurer une s�curit� satisfaisante
est plus grande que la taille des cl�s en cryptographie � cl�
secr�te. En fait la notion et l'importance de la taille de cl� pour
assurer la s�curit� n'est l�gitime que dans le cas de la cl�
secr�te. En effet ces syst�mes reposent sur l'hypoth�se que les
seules attaques possible sont ce que l'on nomme les attaques
exhaustives qui consitent � �num�rer toutes les cl�s possibles.
Par exemple dans le cas d'une cl� de 128bits, la
taille de l'espace � �num�rer est 2128.
En revanche dans le cas de la cl� publique, la taille de cl� n'a de
l�gitimit� que lorsqu'on consid�re le m�me syst�me. En effet, par
exemple le syst�me RSA de 512 bits est bien moins s�r qu'un AES de 128
bits. La seule mesure l�gitime pour �valuer un cryptosyst�me � cl�
publique est la complexit� de la meilleure attaque connue. Ce qui fait
toute la diff�rence on n'est jamais � l'abri de perc�es th�oriques.
Tr�s r�cemment un groupe de chercheurs est parvenu �
factoriser un nombre de 512 bits. En cons�quence, pour avoir une
s�curit� suffisante pour les ann�es � venir, on conseille g�n�ralement
d'utiliser des nombres n de 1024 bits.
En chiffrement, il vaut donc mieux utiliser des algorithmes de
chiffrement � cl� secr�te quand c'est possible. Une solution tout �
fait int�ressante et acceptable est le compromis �labor� par
Zimmermann pour concevoir PGP. Le principe du chiffrement est le
suivant : supposons qu'Alice et Bob souhaitent communiquer de mani�re
int�gre, en utilisant un algorithme � cl� secr�te - en l'occurence,
pour PGP, c'est l'algorithme IDEA.
- Alice et Bob se mettent d'accord sur la cl� secr�te par un
protocole d'�change de cl�s. Ce genre de protocole utilise des
propri�t�s de cryptographie � cl� publique. Un des plus c�l�bres
en la mati�re est le protocole de Diffie-Hellman.
- Ensuite ils communiquent en utilisant l'algorithme IDEA qui
est publique.
Une fois que leur conversation est termin�e, ils jettent la cl� de
session. Un tel syst�me combine les avantages des deux types de
crytographie. En g�n�ral, on consid�re que le maillon faible est le
protocole d'�change de cl�s.
Bibliographie
Histoire de la cryptographie :
- S. Singh : Histoire des codes secrets. Jean-Claude
Latt�s, 1999.
- D. Kahn : The Codebreakers: the story of secret
writing. MacMillan publishing, 1996.
Pour l'AES :
Cryptographie en g�n�ral :




