Introdu��o � criptografia
ArticleCategory:
System Administration
AuthorImage:

TranslationInfo:[Author and translation history]
original in fr Pierre
Loidreau
fr to en Axelle
Apvrille
en to pt Bruno
Sousa
AboutTheAuthor
O Pierre trabalha como professor-Investigador na ENSTA (Escola
Nacional Superior de T�cnicas Avan�adas). O seu campo de investiga��o
diz respeito a "sistemas encriptados" baseados na teoria de correc��o
de erros. "Joga" com o linux todos os dias... e t�nis muito
frequentemente.
Abstract:
Este artigo foi publicado primeiro numa revista de Linux Francesa,
numa edi��o especial focando a seguran�a. O editor, os autores, os
tradutores, gentilmente, permitiram a LinuxFocus de publicar cada
artigo desta edi��o especial. De acordo, a LinuxFocus apresentar-lhos-�
mal estejam traduzidos para Ingl�s. Obrigado a todas as pessoas
envolvidas neste trabalho. Este gen�rico ser� reproduzido para cada
artigo tendo a mesma origem.
ArticleIllustration:

ArticleBody:[The article body]
O porqu� da criptografia - 2500 anos de hist�ria.
A origem da criptografia, provavelmente, remonta ao princ�pios da
exist�ncia humana, logo que as pessoas tenham tentado aprender a
comunicar. Consequentemente, tiveram de encontrar meios para garantir a
confidencialidade de parte das suas comunica��es. Contudo o primeiro
uso deliberado de m�todos t�cnicos para encriptar mensagens pode ser
atr�buido aos antigos Gregos, em meados do s�culo VI A.C. uma vara,
chamada "scytale" foi utilizada. O emissor enrolaria uma peda�o de
papel � volta da vara e escreveria a sua mensagem longitudinalmente
nela. Depois abria o papel e envi�va-o para o endere�o respectivo. A
desencripta��o da mensagem sem o conhecimento do comprimento das varas
- actuando aqui como uma chave secreta - era considerado imposs�vel.
Mais tarde os romanos utilizaram o c�digo cifrado de C�sar para
comunicar (uma terceira letra do alfabeto).
Os pr�ximos 19 s�culos foram devotados � cria��o de t�cnicas de
encripta��o experimentais, inteligentes, em que, cuja seguran�a,
actualmente, reside no quanto o utilizador confia nelas. Durante o
s�culo XIX, o Kerchoffs escreveu os princ�pios da encripta��o moderna.
Um destes princ�pios afirmava que a seguran�a de um sistema encriptado
n�o residia no processo de encripta��o em si, mas sim na chave que era
utilizada.
Assim, deste ponto de vista, era esperado que os sistemas de
encripta��o seguissem estes requisitos. Contudo, os sistemas
existentes, ainda carecem de c�lculos matem�ticos e por conseguinte,
de utilit�rios para medir o benchmark de resist�ncia a ataques. Melhor
seria se algu�m atingisse o objectivo mor da criptografia e encontrasse
um sistema, incondicionalmente, 100% seguro ! Em 1948 e 1948, foram
adicionadas bases cient�ficas � criptografia com 2 papeis de Claude
Shannon: "Uma Teoria Matem�tica da Comunica��o" e, principalmente, "A
Teoria de Comunica��o de Sistemas Secretos". Estes artigos afastaram
esperan�as e preconceitos. O Shannon provou a cifra��o de Vernam que
havia sido proposta alguns anos antes - e tamb�m a renomeou para One
Time Pad -- era o �nico sistema, incondicionalmente, seguro que alguma
podia existir. Infelizmente, tal sistema n�o era poss�vel p�-lo em
pr�tica... Esta � a raz�o porque, nos nossos dias, a evolu��o dos
sistemas de seguran�a � baseada em seguran�a computacional. Um defende
que a chave de cifra��o � segura se nenhum ataque conhecido n�o fa�a
mais do que procurar por todas as chaves poss�veis.
AES (Padr�o avan�ado de Encripta��o)
Recentemente, em Outubro de 2000, o NIST (National Institute of
Standards and Technology) anunciou um novo padr�o de uma chave secreta
de cifragem, escolhido de 15 candidatos. Este novo padr�o pretendia
substituir o velho algoritmo DES, cujo tamanho das chaves se est� a
tornar muito pequeno. O Rijndael - um nome comprimido, origin�rio dos
seus inventores Rijmen e Daemen - foi escolhido para se tornar o futuro
AES.
Este sistema de encripta��o � dito ser um "bloco" de cifragem � medida
que as mensagens s�o encriptadas em blocos inteiros, com unidades de
128-bits. Existem m�ltiplas ideias que prop�em a utiliza��o de chaves
com 128, 192, 256 bits. S� para sua informa��o, o DES encripta blocos
de 64 bits com uma chave de 56 bits. O DES triplo, normalmente,
encripta blocos de 64 bits com uma chave de 112 bits.
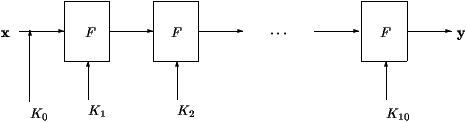
Tabela 1: Iterac��es do AES
O modo operacional do AES est� descrito na figura 1. Primeiro uma
chave secreta K0 � ajustada bit a bit � mensagem. Depois,
semelhantemente a todos os blocos de cifragem. A fun��o F � iterada,
utilizando sub-chaves geradas a partir de uma rotina de expans�o,
inicializada pela chave m�e.
Para o AES, a fun��o F � iterada 10 vezes.
- A figura 2 descreve o modo como a fun��o F � iterada para a
encripta��o. Recebe um bloco de 128-bits reparticionados em 16
octetos. Primeiro a substitui�o S � aplicada a cada byte (octeto).
De seguida a permuta��o P � aplicada aos 16 octetos. A sub-chave de
128-bit, gerada pela rotina de expans�o, � adicionada bit a bit ao
resultado anterior.
- A chave Ki do ciclo n°i � obtida da chave da rotina de
expans�o utilizando a sub-chave K(i-1) do ciclo n°i-1 sendo K0 a
chave secreta. A rotina de expans�o da chave est� descrita na figura
3. Os 16 bytes da chave K(i-1) s�o processadas 4 a 4.
Os �ltimos 4 bytes s�o permutados utilizando a substitui��o S - a
mesma substitui��o que � utilizada na fun��o iterada F para
substituir os bits de cada octeto. Depois os primeiros 4 bytes
resultantes s�o adicionados ao elemento alpha i. Este elemento � o
byte de pr�-defini��o que depende do iterador do ciclo. Finalmente,
para obter o Ki, os 4 bytes resultantes s�o adicionados bit a bit aos
primeiros 4 bytes do K(i-1). De seguida o resultado � adicionado aos
pr�ximos quatro bytes, etc.
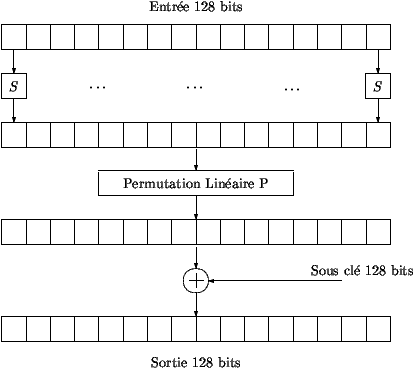
Tabela 2: Fun��o F F
Vejemos, agora, muito resumidamente, como as substitui��es s�o
constru�das e ao que corresponde a constante ai.
Tecnimente - e por raz�es de simplifica��o - um octeto deve ser
considerado como um elemento conjunto de 256 elementos, chamado um
campo finito e no qual todas as opera��es simples (como a adi��o,
multiplica��o, e inverso) existem.
De facto a pr�via substitui��o S � o inverso de tal campo. A
substitui��o S � especificada como sendo uma opera��o simples e pode,
facilmente, ser implementada.
O elemento ai corresponde
� eleva��o da pot�ncia i de um elemento do campo. Tais considera��es
tornam as implementa��es do AES muito eficientes.
Como o AES � somente constru�do atrav�s de opera��es de bitwise, isto
d�-lhe duas grandes vantagens:
- mesmo puras implementa��es em software do AES s�o bastante
r�pidas. Por exemplo uma implementa��o em C++ num Pentium a 200 Mhz
oferece uma performance de 70Mbits/s de encripta��o ;
- a resist�ncia do AES a uma an�lise de encripta��o diferencial e
linear n�o depende da escolha da S-Box, como para o DES tais S-Boxes
eram suspeitas de conter uma backdoor para o NSA. De facto, todas as
opera��es s�o simples.
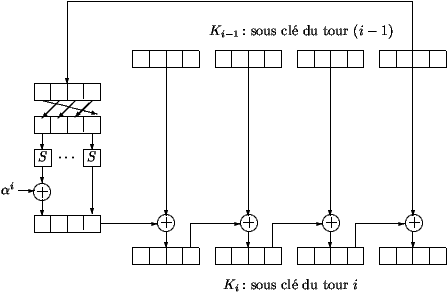
Tabela 3: Rotina da Chave de expans�o
Chave P�blica de encripta��o
Em 1976, o Diffie e o Hellman publicaram um artigo "New Directions in
Cryptography" o qual era um objectivo real para a comunidade dos
cript�grafos. Este artigo introduzia o conceito de chave p�blica de
encripta��o. Naquela altura, a �nica familia de algoritmos conhecida -
algoritmos de chaves secretas sim�tricas - n�o podia mais satisfazer as
novas necessidades que apareciam devido � explos�o dos m�todos de
comunica��o como as redes.
Basicamente, o princ�pio da sua nova ideia foi a introdu��o do
conceito de fun��es de um s� sentido trapdoor. Tais fun��es operam
facilmente num sentido mas computacionalmente imposs�vel de inverter
sem o conhecimento de um segredo chamado trap - mesmo que a fun��o seja
conhecida por todos. Ent�o, a chave p�blica actua como fun��o enquanto
que o trap (somente conhecido por um n�mero limitado de utilizadores) �
chamada chave privada. Isto deu origem ao nascimento ao mundo da Alice,
Bob (e outros). A Alice e o Bob s�o duas pessoas que tentam comunicar
com requisitos de integridade, evitando intrusos que podem tentar
escutar ou at� mesmo alterar a comunca��o.
Claro que, para decrifrar a mensagem , o recipiente s� precisa de
inverter a fun��o utilizando o segredo denominado trap.
O exemplo mais simp�tico do criptografismo p�blico (e, sem d�vida o
mais simples) foi apresentado dois anos mais tarde em 1978. Foi
inventado por Rivest, Shamir e Adleman e por aqui surgiu o RSA. �
baseado na dificuldade matem�tica da factoriza��o inteira. A chave
privada � feita do tripleto (p,q,d) com p e q dois primos (tendo
aproximadamente o mesmo tamanho), e d � um primo relativo de
p-1 e q-1. A chave p�blica � formada pelo par (n,e), com
n=pq, e e o inverso do m�dulo de d (p-1)(q-1), por exemplo
ed = 1 mod(p-1)(q-1).
Suponha que a Alice quer enviar algum texto, encriptada com a chave
p�blica do Bob(n,e). Primeiro, transforma a mensagem num inteiro m
menos o n. Depois, processa
c = me mod
n,
e envia o resultado c para o Bob. Do seu lado, o Bob, cuja chave
privada � (p,q,d), processa :
cd mod n =
med mod n =
m.
Para o RSA, a fun��o armadilha de um s� sentido � a fun��o que associa
um inteiro x <n ao valor xe mod n.
Desde o RSA, muitos outros sistemas chave de encripta��o p�blicos foram
inventados. Presentemente uma das alternativas mais famoasas ao RSA �
um sistema de encripta��o baseado em logatimos discretos.
Utiliza��o Moderna da Criptografia
Actualmente a chave p�blica de criptografia � realmente interessante
porque � f�cil de utilizar e resolve muitos problemas de seguran�a at�
ent�o sem resolu��o. Mais precisamente, resolve alguns problemas de
autentica��o:
- Identificando Individuos: a utiliza��o das comunica��es
an�nimas hoje tem o seguinte significado, a Alice quer ter a certeza
que a pessoa com quem est� a falar n�o est� a enganar ou a persuadir
o Bob. Para tal fazer, ela utiliza um protocolo de identifica��o.
Existem m�ltiplos protocolos que, no geral, assentam nos princ�pios
da RSA ou do algoritmo discreto.
- Autentica��o de Documentos: uma autoridade autentica um
documento atrav�s de uma assinatura digital. A assinatura consiste
em adicionar alguns bits resultantes de algum processamento do
documento e da autoridade como entrada e, geralmente encontram-se na
forma de hash, atrav�s de um algoritmo de hash como o MD5 ou o SHA.
Assim, qualquer pessoa com acesso ao documento devia ser capaz de
verificar que assinatura foi atribuida pela autoridade. Para tal,
esquemas de assinatura, s�o utilizados. Um dos mais famosos esquemas
de assinaturas � o ElGamal - mais uma vez baseado nos problemas de
logaritmos discretos.
Para al�m da chave secreta de encripta��o, a chave-p�blica de
encripta��o fornece encripta��o � base de sistemas de cripta��o,
garantindo confidencialidade nas comunica��es.
Imaginemos que a Alice quer comunicar secretamente com o Bob. A Alice
obtem a chave p�blica do Bob num direct�rio p�blico e, encripta a sua
mensagem com esta chave. Quando o Bob recebe o texto encriptado, ele
usa a chave privada para decifrar o texto encriptado e l� o texto
inicialmente limpo. Ambas as chaves t�m regras diferentes, isto explica
por que tais sistemas s�o designados de sistemas de encripta��o
assim�tricos - referindo os sistemas com chave de encripta��o para
cifrar e decifrar s�o conhecidos como sistema de encripta��o
sim�tricos.
A chave p�blica de encripta��o oferece um outro grande benef�cio em
rela��o � chave secreta de encripta��o. De facto, se n utilizadores
comunicarem atrav�s de uma chave encriptada secreta, cada um deles
precisa de uma chave diferente para cada pessoa no grupo. Assim, t�m de
ser arranjadas n(n-1) chaves. Se o n representa milhares de
utilizadores ent�o milh�es de chaves precisam de ser arranjadas... Para
al�m disto, adicionar um utilizador ao grupo n�o � tarefa f�cil, porque
novas n chaves precisam de ser geradas para o utilizador poder
comunicar com todos os membros do grupo. Depois, estas novas chaves
precisam de ser enviadas de volta para o grupo. De modo contr�rio, nos
sistemas de encripta��o assim�tricos, as n chaves p�blicas dos membros
s�o arquivadas num direct�rio p�blico. Adicionar um novo utilizador,
consiste, simplesmente, em adicionar a sua chave p�blica ao direct�rio.
Usar uma chave p�blica ou privada: encontrando a melhor combina��o
O par�grafo anterior explicou que a chave p�blica de encripta��o
resolveu muitos problemas com os quais a chave privada n�o conseguia
lidar. Pode questionar-se porque � que foi desenhado o AES.
Actualmente, existem duas grandes explica��es para esta escolha.
- Primeiro, uma raz�o pr�tica. Geralmente, os sistemas de
encripta��o com chave p�blica s�o muito lentos. Por exemplo, as
implementa��es de software do RSA s�o mil vezes mais lentas que o
AES, e o RSA n�o foi desenhado tendo em mente a implementa��o de
hardware. A transmiss�o de informa��o � t�o crucial nos dias de hoje
que n�o podemos estar limitados por um algoritmo secreto.
- Segundo, o n�cleo da estrutura dos sistemas de encripta��o
com chave p�blica conduz a outros problemas de seguran�a.
Por exemplo, os sistemas de encripta��o com uma chave p�blica
requerem tamanhos de chaves maiores - para um n�vel de seguran�a
correcto - que os sistemas de encripta��o com chave secreta.
Actualmente a ideia e import�ncia do tamanho da chave dos sistemas
de encripta��o s� deve ser considerada nos sistemas de encripta��o
com chave secreta. De facto, tais sistemas assentam no facto que s�
ataques de for�a-bruta � que os pode derrotar, ou seja enumerando
todas as possibilidades para as chaves. Se o tamanho da chave for de
128 bits ent�o devem ser enumeradas 2128
possibilidades.
Mas com os sistemas de encripta��o de chave p�blica, o tamanho da
chave s� � interessante quando se considera o mesmo sistema. Por
exemplo, o RSA com uma chave de 512 bit � menos seguro que o AES
com uma chave de 128 bit. O �nico modo correcto de avaliar um sistema
de encripta��o de chave p�blica � estimar a complexidade do ataque
mais bem conhecido e, isto � ligeiramente diferente: um nunca sabe se
uma nova inven��o vai comprometer a seguran�a do sistema.
Recentemente, um grupo de pesquisadores, facturizou, com sucesso, um
inteiro de 512 bit. Consequentemente, para um n�vel correcto de
seguran�a, o conselho normal � utilizar n�meros de 1024 bits.
Por conseguinte, para pura encripta��o, os algoritmos de chave secreta
s�o preferidos- quando � poss�vel utiliz�-los. Zimmermann trabalhou sob
uma solu��o h�brida interessante, implementada no PGP. Basicamente
quando a Alice e o Bob querem comunicar com factores de integridade
utilizando o algoritmo de chave secreta (o PGP usa o IDEA):
- A Alice e o Bob negoceiam uma chave utilizando um protocolo
de troca de chaves. Os protocolos de troca de chaves utilizam chaves
de encripta��o p�blica. Um dos mais famosos protocolos assenta no
algoritmo de Diffie-Hellman's.
- Depois, comunicam utilizando o algoritmo IDEA.
Quando a comunica��o termina, a chave de negocia��o da sess�o �
descartada. Tais sistemas usam ambas as chaves secretas e p�blicas dos
sistemas de encripta��o. Normalmente, as pessoas consideram como sendo
a parte mais insegura o protocolo de troca das chaves.
Bibliografia
Hist�ria da Criptografia:
- S. Singh : Histoire des codes secrets. Jean-Claude
Lattès, 1999.
- D. Kahn : The Codebreakers: the story of secret
writing. MacMillan publishing, 1996.
Para o AES :
Criptografia em geral:





